Activity related to Area of parallelogram and triangle for class 9th

Activity related to to find a relation, between the areas of two parallelograms on the same base and between the same parallels.

Let us take a graph sheet and draw two parallelograms ABCD and PQCD on it as shown in Fig

Now find the areas of these two parallelograms by counting the number of complete squares enclosed by the figure, the number of squares a having more than half their parts enclosed by the figure and the number of squares having half their parts enclosed by the figure. The squares whose less than half parts are enclosed by the figure are ignored.
You will find that areas of both the parallelograms are (approximately) 15 Sq.cm

Hence, you to conclude that parallelograms on the same base and between the same parallels are equal in area

Theorem : Parallelograms on the same base and between the same parallels are equal in area.

Proof : Two parallelograms ABCD and EFCD, on the same base DC and between the same parallels

AF and DC are given (see Fig).
We need to prove that ar (ABCD) = ar (EFCD).
In Δ ADE and Δ BCF,
∠ DAE = ∠ CBF (Corresponding angles from AD || BC and transversal AF) (1)
∠ AED = ∠ BFC (Corresponding angles from ED || FC and transversal AF) (2)
Therefore, ∠ ADE = ∠ BCF (Angle sum property of a triangle) (3)
Also, AD = BC (Opposite sides of the parallelogram ABCD) (4)
So, Δ ADE ≅ Δ BCF [By ASA rule, using (1), (3), and (4)]
Therefore, ar (ADE) = ar (BCF) (Congruent figures have equal areas) (5)
Now,adding ar (EDCB) both the sides
 ar (ADE) + ar (EDCB) = ar (BCF)+ ar (EDCB)
                 ar (ABCD) = ar (EFCD)
So, parallelograms ABCD and EFCD are equal in area.

Problem: If a triangle and a parallelogram are on the same base and between the same parallels, then prove that the area of the triangle is equal to half the area of the parallelogram.
Solution : Let Δ ABP and parallelogram ABCD be on the same base AB and between the same parallels
AB and PC (see Fig).

To prove :  ar (PAB) =1/2 ar (ABCD)
Construction: Draw BQ || AP to obtain another parallelogram ABQP. So that parallelograms ABQP
and ABCD will be on the same base AB and between the same parallels AB and PC.
Therefore, ar (ABQP) = ar (ABCD) (By Theorem that parallelograms on the same base and between the same parallels are equal in area) --------(1)

But Δ PAB ≅ Δ BQP (As diagonal PB divides parallelogram ABQP into two congruent triangles.)

So, ar (PAB) = ar (BQP) -------------(2)

Therefore, ar (PAB) =1/2ar (ABQP) [From (2)]--------------------- (3)

This gives ar (PAB) =1/2 ar (ABCD) [From (1) and (3)]

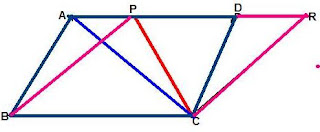
Theorem :Two triangles on the same base (or equal bases) and between the same parallels are equal in area.

Let two triangles ABC and PBC on the same base BC and between the same parallels BC and AP

Construction : Draw CD || BA and CR || BP such that D and R lie on line AP(see Fig) to get two parallelograms PBCR and ABCD on the same base BC and between the same parallels BC and AR.

Now, Parallelograms PBCR and ABCD on the same base BC and between the same parallels BC and AR. Therefore, ar (ABCD) = ar (PBCR) ----------(1)

Now Δ ABC ≅ Δ CDA and Δ PBC ≅ Δ CRP ( The diagonals of a parallelogram divides it  into two congruent triangles)

So, ar(Δ ABC) = ar(Δ CDA) and ---------(ii)

ar (ABCD) = ar(Δ ABC) + ar(Δ CDA) --------------(iii)

ar (PBCR)  = ar(Δ PBC) = ar(ΔCRP) ----------------(iv)

From (1),(ii),(iii) and (iv) , we have 

So, ar (ABC) =1/2 ar (ABCD)

and ar (PBC) =1/2 ar (PBCR)

Therefore, ar (ABC) = ar (PBC)

Problem: A farmer was having a field in the form of a parallelogram PQRS. She took any point A

on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?

When she took any point A on RS and joined it to points P and Q

A divides the field into three parts. These parts are triangular in shape –> ∆PSA, ∆PAQ and ∆QRA 

So, Area of   IIgm  PQRS =  Area of ∆PSA + Area of ∆PAQ + Area of ∆QRA  ... (1)  

∴ Area (∆PAQ) = 1/2 area (PQRS)      ... (2) [a parallelogram and triangle are on the same base and 

between the same parallels, the area of triangle is half the area of the parallelogram]

From equations (1) and (2), we get

Area (∆PSA) + area (∆QRA) + 1/2 area (PQRS) = area (PQRS)   

Area (∆PSA) + area (∆QRA)=  area (PQRS) -1/2 area (PQRS) 

Area (∆PSA) + area (∆QRA)=  1/2 area (PQRS) 

Area (∆PSA) + area (∆QRA)= Area (∆PAQ)

Clearly, farmer must sow wheat in triangular part PAQ and pulses in other two triangular parts PSA and QRA or wheat in triangular part PSA and QRA and pulses in triangular parts PAQ.

Class-IX. Math. Chapter : Area of Parallelogram and Triangles. NCERT Solutions Topperlearning Download
9th Area of Parallelogram and Triangle Test paper