CBSE/NCERT TEST PAPER MATHEMATICS (Class-10) Circle

I. Fill in the blanks. 

a. The word ‘tangent’ comes from the Latin word ------------ 

b. A tangent to a circle intersects it in ----------- point (s).

c. A line intersecting a circle in two points is called a --------

d. A circle can have -----------parallel tangents at the most.

e. The common point of a tangent to a circle and the circle is called ----------

2. Solve these questions (any five) 4X5=20

1. Prove that The tangent at any point of a circle is perpendicular to the radius through the point of contact

2. Prove that the lengths of tangents drawn from an external point to a circle are equal. 

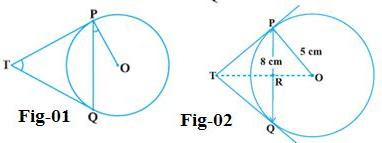
3. Two tangents TP and TQ are drawn to a circle with centre O from an external point T.(see fig. 1) Prove that < PTQ = 2 < OPQ. 

4. PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (see Fig. 2) Find the length TP. 

5. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle. 

6. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre. 

7. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

8. A triangle PQR is drawn to circumscribe a circle of radius 4cm. The circle touches QR at D such that   QD = 6 cm and RD = 8 cm. Find PQ and PR.

9. The tangent at a point C of a circle and a diameter AB when extended intersect at P. If <PCA = 110⁰ , find < CBA.

10. In the figure. X.Y. are two parallel tangents to a circle with Center O and another tangent AB with point of contact C intersecting XY at A and X.Y. at B. Prove that <AOB = 90⁰.